当变量消失之时
在之前的文章中,我们介绍过一些关于函数式编程的内容,众所周知,函数式的一大特点是不可变,而结构化编程中的循环结构通常需要变量驱动迭代,所以在函数式编程中需要使用递归取代通常意义上的循环。接下来,让我们尝试不使用变量来完成函数式编程中常用的「循环」函数。
不可变的优势
「变量不可变」这种自我限制行为能给我们带来什么?
首先,最大的收益是线程安全性。在现代编程中,我们常常需要通过多线程来处理高并发以及充分利用 CPU 多核心的优势。传统解决方案通常使用共享内存来实现线程间通信,然后使用锁来进行线程同步。然而,这种方式并不易于使用,甚至可能导致死锁问题。此外,频繁使用锁也会对性能造成不利影响。然而,当变量不可变时,问题本身也随之消失:所有的竞态、死锁、同步问题都源于可变变量,如果变量不再被更新,就不会出现竞态与同步问题;没有用来限制可变变量的锁,也就不会发生死锁。
例如,函数式语言 Erlang/Elixir 就使用了 Actor 模型来解决并发编程的问题,这种模型通过消息传递而不是共享内存来进行通信,从而避免了许多线程安全性的问题。
此外,由于不需要考虑状态的变化,阅读、编写和调试代码变得更为简洁直观;同时,编译器和运行时环境更容易对代码进行优化,以提高运行效率。
这并不是纸上谈兵。在最基本的编程语言语法层面上,现代编程语言都更偏向 val、let、const 而不是 const auto、final var。也就是说,通过简化常量声明方式,使人们在心理上更容易接受常量,很明显,没有人愿意重复书写 const T *const 这种繁琐的常量类型。同理,mut foo: &mut T 这种繁琐的变量声明方式也会逼迫人们选择使用常量将其代替。说到底,这是一种默认思路的转变:从「常量只是一种限制变量的修饰」到「纯函数式的世界里只有常量,不过有时可以不那么纯」。
向上看去,便来到了不可变对象与数据结构,所谓「不可变」的意思是在被创建后,其结构内部各属性或字段都不能通过任何方式进行修改,但可以通过创建新的对象来取代旧对象,显然,这些对象天然线程安全,并且其方法皆为无副作用的纯函数。比较常见的例子有字符串、时间处理相关等。
import java.time.LocalDate
fun main() {
val today = LocalDate.now();
val oneYearLater = today.plusYears(1);
println("today: $today, oneYearLater: $oneYearLater")
println(oneYearLater.dayOfWeek)
// today: 2024-04-19, oneYearLater: 2025-04-19
// SATURDAY
}与读作 Kotlin,写作 Java 的 LocalDate 形成鲜明对比的便是仅在 10 天内就(不得已)吸取了 Java 不少糟粕,并直到 29 年后的今日仍纠缠不清的 JavaScript 的 Date。(java.util.Date:口黑,亻尔女子!)1
const today = new Date()
today.setFullYear(today.getFullYear() + 1)
console.log(`oneYearLater: ${today.toDateString()}`)
console.log(today.getDay())
// oneYearLater: Sat Apr 19 2025
// 6虽然没有自己的时间处理方案,但得益于对 Scala 的大量借鉴,Kotlin 有着一整套可变与不可变的集合类,任君选择。
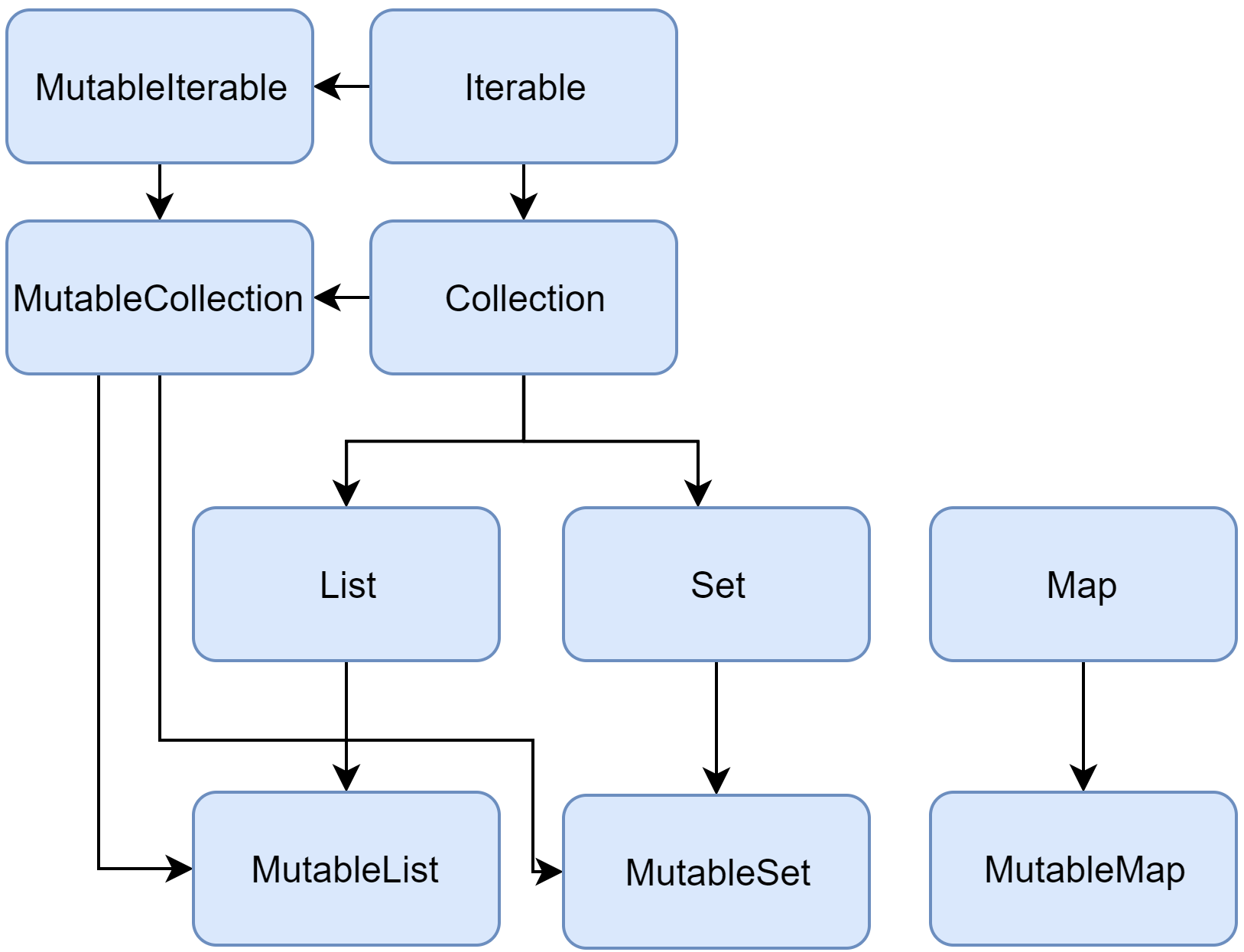
写到这里,便回忆起一件自己亲身经历过的「噩梦」:(好吧,其实就是为了这点馅包了这锅 🥟。)
const regex = /foo/g
const s = 'play football'
console.log(regex.test(s))
console.log(regex.test(s))这段代码的作用是利用正则表达式检测字符串中是否含有「foo」,程序运行结果显而易见,
true
true吗?
true
false「想象另一种结果:第一次,白球将黑球撞入洞内;第二次,黑球走偏了;第三次,黑球飞上了天花板;第四次,黑球像一只受惊的麻雀在房间里乱飞,最后钻进了您的衣袋;第五次,黑球以接近光速的速度飞出,把台球桌沿撞出一个缺口,击穿了墙壁,然后飞出地球,飞出太阳系,就像阿西莫夫描写的那样。这时您怎么想?
……
「这就意味着宇宙普适的物理规律不存在,那物理学……也不存在了。」
⸺《三体》
实不相瞒,这段样例正是源于博客处理脚注的代码,在那个月黑风高的夜晚,当遇到这个难以置信的玄学幽灵事件时,我的心情就是「计算机科学不存在了」。
言归正传,真相其实很简单,当你知道有 lastIndex 这种万恶之源存在时:
const regex = /foo/g
const s = 'play football'
console.log(regex.test(s), regex.lastIndex)
console.log(regex.test(s), regex.lastIndex)
// true 8
// false 0简单来说,const regex = /foo/g 并不只是单纯地定义一个正则表达式字面量,而是实例化了一个 RegExp 对象,而其中的 lastIndex 属性会随着方法调用而随之变化。虽然从面向对象的角度来看可能没有什么问题,但不纯粹就是坏文明!(下次一定仔细阅读文档。)
还是来看看 Kotlin 吧:
fun main() {
val regex = Regex("/foo/g")
val s = "play football"
println(regex.containsMatchIn(s))
println(regex.containsMatchIn(s))
// false
// false
}你看,这种不可变对象就用起来很放心。
顺带一提,虽然刚刚吐槽了 JS 的 Date,但新的日期处理方案 Temporal 指日可待。目前该提案马上进入 Stage 4,之前我在项目 SubMGR 中也通过引入 polyfill 提前进行了体验,非常好用。
继续向上,函数式思想对框架领域也有着深刻影响。如前端的标志性框架 React:
const [names, setNames] = useState(['BioniCosmos'])
// Wrong!
// names.push('Daniel')
// Correct!
setNames([...names, 'Daniel'])以及大数据领域的 Spark、Hadoop。(这方面就不太了解啦。)
知道了各种优点,接下来就让我们先来看看递归的威力。
递归取代循环
对于初学者来说,递归可能是一种较为抽象的思想,只可意会,不可言传,相比之下,循环更为简单直接,特别是对于像「输出 0—9 十个数」这样的任务。然而,一旦熟悉了递归,就会发现它的简洁和强大之处。
废话少说,我们直接来看第一个例子:斐波那契数列。
public class Fibonacci {
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
var a = 0;
var b = 1;
var c = 0;
for (var i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return c;
}
}fib n
| n <= 1 = n
| otherwise = fib (n - 1) + fib (n - 2)感觉如何?没过瘾?那再把第二个例子⸺快速排序端上来吧。
public class QuickSort {
public static void quickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
private static void quickSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
var pivot = partition(arr, left, right);
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
private static int partition(int[] arr, int left, int right) {
var pivot = arr[right];
var i = left - 1;
for (var j = left; j < right; j++) {
if (arr[j] <= pivot) {
i += 1;
swap(arr, i, j);
}
}
i += 1;
swap(arr, i, right);
return i;
}
private static void swap(int[] arr, int i, int j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}quickSort [] = []
quickSort (x : xs) =
quickSort (filter (<= x) xs)
++ [x]
++ quickSort (filter (> x) xs)我承认这场比赛称不上公平,例子也有些文不对题,但节目效果应该是达到了。不管怎么说,递归与函数式实在是优雅。
既然有了「递归」这把利器,我们就可以正式开始实现那些耳熟能详的函数了。
实现常用函数
接下来介绍的所有函数将分别使用 TypeScript、Kotlin、Haskell、Elixir、Racket 五门语言编写。
reduce
传说中,掌握了 reduce 就掌握了一切。
reduce 函数是函数式编程中的一个重要高阶函数,它的作用是将一个集合中的所有元素按照指定的规则进行归约,最终得到一个单一的结果。使用循环实现 reduce 的代码如下:
const reduce = <T, U>(f: (acc: U, x: T) => U, init: U, xs: T[]): U => {
let acc = init
for (const x of xs) {
acc = f(acc, x)
}
return acc
}那么使用递归应该如何实现呢?
- 将第一个元素传入
f中。 - 将
f的返回值和剩余元素传入reduce中继续运算。 - 重复上述过程,直到集合中只剩下一个元素,此时终止递归并直接返回
f调用后的返回值即可。
将每一步展开后的代码过程如下:
const f = (acc, x) => acc + x
reduce(f, 0, [1, 2, 3])
// (0, 1) => 0 + 1
reduce(f, 1, [2, 3])
// (1, 2) => 1 + 2
reduce(f, 3, [3])
// (3, 3) => 3 + 3
reduce(f, 6, [])
// return 6TypeScript
const reduce = <T, U>(f: (acc: U, x: T) => U, init: U, list: T[]): U => {
if (list.length === 0) {
return init
}
const [x, ...xs] = list
return reduce(f, f(init, x), xs)
}Kotlin
tailrec fun <T, U> List<T>.reduce(init: U, f: (U, T) -> U): U {
if (this.isEmpty()) {
return init
}
val x = this.first()
val xs = this.drop(1)
return xs.reduce(f(init, x), f)
}Haskell
reduce f init [] = init
reduce f init (x : xs) = reduce f (f init x) xsElixir
def reduce([], init, _), do: init
def reduce([x | xs], init, f), do: reduce(xs, f.(x, init), f)Racket
(define/match (reduce f init _xs)
[(_ _ (list)) init]
[(_ _ (cons x xs)) (reduce f (f init x) xs)])map
map 映射函数是一个我很喜欢的函数,因为它能直观地体现出数据在函数间流转处理的过程。map 常用于集合结构,也可用于 Monad,其作用为将类型 T 转换(映射)到类型 U。
相比于 reduce,map 用法单一,实现上也更为简单。循环实现如下:
const map = <T, U>(f: (x: T) => U, xs: T[]): U[] => {
const mapped = Array.of<U>()
for (const x of xs) {
mapped.push(f(x))
}
return mapped
}若不使用循环,既可以用万能的 reduce 也可以直接用递归实现,实现思路与循环并无区别,只不过将 push 替换为拼接。
TypeScript
const map = <T, U>(f: (x: T) => U, xs: T[]): U[] =>
reduce((acc, x) => [...acc, f(x)], Array.of(), xs)const map = <T, U>(f: (x: T) => U, list: T[]): U[] => {
if (list.length === 0) {
return []
}
const [x, ...xs] = list
return [f(x), ...map(f, xs)]
}Kotlin
fun <T, U> List<T>.map(f: (T) -> U): List<U> =
this.reduce(listOf()) { acc, x -> acc + f(x) }fun <T, U> List<T>.map(f: (T) -> U): List<U> {
if (this.isEmpty()) {
return listOf()
}
val x = this.first()
val xs = this.drop(1)
return listOf(f(x)) + xs.map(f)
}Haskell
map f = reduce (\acc x -> acc ++ [f x]) []map f [] = []
map f (x : xs) = f x : map f xsElixir
def map(xs, f), do: reduce(xs, [], fn x, acc -> acc ++ [f.(x)] end)def map([], _), do: []
def map([x | xs], f), do: [f.(x) | map(xs, f)]Racket
(define (map f xs)
(reduce (lambda (acc x) (append acc (list (f x)))) null xs))(define/match (map f _xs)
[(_ (list)) null]
[(_ (cons x xs)) (cons (f x) (map f xs))])filter
接下来是 filter,它能够根据指定的条件筛选出符合条件的元素。
const filter = <T>(f: (x: T) => boolean, xs: T[]): T[] => {
const filtered = Array.of<T>()
for (const x of xs) {
if (f(x)) {
filtered.push(x)
}
}
return filtered
}TypeScript
const filter = <T>(f: (x: T) => boolean, xs: T[]): T[] =>
reduce((acc, x) => (f(x) ? [...acc, x] : acc), Array.of(), xs)const filter = <T>(f: (x: T) => boolean, list: T[]): T[] => {
if (list.length === 0) {
return []
}
const [x, ...xs] = list
return f(x) ? [x, ...filter(f, xs)] : filter(f, xs)
}Kotlin
fun <T> List<T>.filter(f: (T) -> Boolean): List<T> =
this.reduce(listOf()) { acc, x -> if (f(x)) acc + x else acc }fun <T> List<T>.filter(f: (T) -> Boolean): List<T> {
if (this.isEmpty()) {
return listOf()
}
val x = this.first()
val xs = this.drop(1)
return if (f(x)) listOf(x) + xs.filter(f) else xs.filter(f)
}Haskell
filter f = reduce (\acc x -> if f x then acc ++ [x] else acc) []filter f [] = []
filter f (x : xs)
| f x = x : filter f xs
| otherwise = filter f xsElixir
def filter(xs, f),
do:
reduce(xs, [], fn x, acc ->
cond do
f.(x) -> acc ++ [x]
true -> acc
end
end)def filter([], _), do: []
def filter([x | xs], f) do
cond do
f.(x) -> [x | filter(xs, f)]
true -> filter(xs, f)
end
endRacket
(define (filter f xs)
(reduce (lambda (acc x) (if (f x) (append acc (list x)) acc)) null xs))(define/match (filter f _xs)
[(_ (list)) null]
[(_ (cons x xs)) (if (f x) (cons x (filter f xs)) (filter f xs))])reverse
关于翻转函数的作用想必无需解释。使用循环实现翻转函数的经典思路是就地交换,这与递归实现差别很大,所以考虑另一种思路:从后向前遍历,将元素推入新的集合中:
const reverse = <T>(xs: T[]): T[] => {
const reversed = Array.of<T>()
for (let i = xs.length - 1; i >= 0; i--) {
reversed.push(xs[i])
}
return reversed
}递归实现思路类似:
- 将集合分为首元素
x和其余元素集合xs。 - 翻转
xs:reverse xs(开始递归)。 - 将
x拼接到翻转后的返回值末尾。
TypeScript
const reverse = <T>(xs: T[]): T[] =>
reduce((acc, x) => [x, ...acc], Array.of(), xs)const reverse = <T>(list: T[]): T[] => {
if (list.length === 0) {
return []
}
const [x, ...xs] = list
return [...reverse(xs), x]
}Kotlin
fun <T> List<T>.reverse(): List<T> =
this.reduce(listOf()) { acc, x -> listOf(x) + acc }fun <T> List<T>.reverse(): List<T> {
if (this.isEmpty()) {
return listOf()
}
val x = this.first()
val xs = this.drop(1)
return xs.reverse() + listOf(x)
}Haskell
reverse = reduce (flip (:)) []不愧是 Haskell,轻易做到了其他语言做不到的事呢。让我们把代码展开以说明其含义。
-
最初形态:
reverse xs = reduce (\acc x -> x : acc) [] xs -
由于 Partial Application,可消除参数
xs:reverse = reduce (\acc x -> x : acc) [] -
观察 lambda 表达式,我们将
:中缀运算符转换为前缀调用形式:reverse = reduce (\acc x -> (:) x acc) [] -
可以发现,lambda 表达式的参数顺序与
:的传入顺序正好相反,遂可以使用flip函数交换参数顺序并直接传入函数(运算符):reverse = reduce (flip (:)) []
直接实现的代码就比较正常了:
reverse [] = []
reverse (x : xs) = reverse xs ++ [x]Elixir
def reverse(xs), do: reduce(xs, [], fn x, acc -> [x | acc] end)def reverse([]), do: []
def reverse([x | xs]), do: reverse(xs) ++ [x]Racket
(define (reverse xs)
(reduce (lambda (acc x) (cons x acc)) null xs))(define/match (reverse _xs)
[((list)) null]
[((cons x xs)) (append (reverse xs) (list x))])有关 reduce 的补充
reduce 很奇特,诸如 map、filter 都有较为明确的用途,但 reduce 似乎什么都能做。
实际上 reduce 和循环极为相似,只不过换了一种形式,又将可变操作转换为不可变操作(如对于列表,push 变为拼接)。
什么?递归是假的?
递归通常比循环更简单、更易理解,这是为什么呢?
- 自然表达:递归更自然地表达了问题的递归结构,特别是对于递归定义的问题(如树、图等),使用递归更符合问题的本质。
- 简洁性:递归能够利用函数的调用栈来管理状态,而不需要额外的变量或控制结构。
- 抽象思维:递归鼓励更抽象的思考方式,可以将问题分解成更小的子问题,使得问题的解决更加清晰和模块化。
那么,代价是什么?
正如第二点所提到的,如果我们将递归分为「展开准备」和「返回应用」两个阶段,在展开过程中,每次对自身的调用都会在调用栈中创建新的帧,如果递归过深,将导致栈区被占满,最终出现 Stack Overflow(栈溢出)错误。此外,函数调用本身也具有一定开销。
怎样才能既使用递归,又保证性能呢?
或许你已经注意到,Kotlin 实现的 reduce 函数比别人多了 tailrec,这个关键字意味着什么?我们使用反编译工具将字节码反编译为 Java 代码,此时会发现,递归竟变成了循环!
public static final Object reduce(@NotNull List $this$reduce, Object init, @NotNull Function2 f) {
Intrinsics.checkNotNullParameter($this$reduce, "<this>");
Intrinsics.checkNotNullParameter(f, "f");
while(!$this$reduce.isEmpty()) {
Object x = CollectionsKt.first($this$reduce);
List xs = CollectionsKt.drop((Iterable)$this$reduce, 1);
Object var5 = f.invoke(init, x);
$this$reduce = xs;
init = var5;
f = f;
}
return init;
}为方便理解,我们将其整理为 Kotlin 代码:
fun <T, U> List<T>.reduce(init: U, f: (U, T) -> U): U {
var list = this
var init = init
while (list.isNotEmpty()) {
val x = list.first()
val xs = list.drop(1)
init = f(init, x)
list = xs
}
return init
}这就是所谓的尾递归优化。
实际上,尾递归优化是递归与尾调用优化(Tail Call Optimization,简称 TCO)相结合的特殊产物。所谓「尾调用」指一个函数里的最后一个动作是返回一个函数的调用结果2,如下所示:
function f() {
const n = nuclearBomb()
return g(n)
}
function g(n: number) {
return n + 1
}这里的函数 f 中的 g(n) 就是尾调用,那么,「优化」又是什么呢?
正常来说,调用新的函数需要创新新的栈帧并将其推入到调用栈中,但由于尾调用已处于函数的最后,当前帧中信息不会被使用,所以被调用函数可以直接重用当前帧而无需创建新帧。
这是一般情况下的 TCO,不难理解。但是,当尾调用变为对自身的递归调用而位置不变(即尾递归)时,优化就变得有趣起来。
对于尾递归优化的效果,想必看了上面 reduce 的例子后不难理解,那么为什么尾递归能够被优化呢?在讨论这个问题之前,我们首先来看另外一个函数⸺isEven 偶数判断:
const isEven = (n: number) => {
if (n === 0) {
return true
}
return !isEven(n - 1)
}这个判断奇偶的思路非常有趣。由于该函数的最后一个操作是逻辑取反 !,所以不构成尾递归。如果想要尾递归,我们必须使 isEven 函数调用作为最后一个操作,于是便有了以下实现:
const isEven = (n: number, even = true) => {
if (n === 0) {
return even
}
return isEven(n - 1, !even)
}当看到尾递归实现时,你会发现原递归实现所具有的那种简洁优雅似乎已不复存在。我们知道,递归之所以简洁是因为它能自动保存运算状态,而循环则需要我们自己使用变量存储状态。显然,尾递归也要遵循计算机科学,既不想手动处理状态又不想影响性能是不可能的。于是,我们只好把变量放到了函数参数的位置上,这就是尾递归的真相。也就是说,借助循环实现的思路就能把 body recursion 改写为 tail recursion。
接下来,执行以下步骤就可以将尾递归优化为循环:
- 函数签名不变。
- 将递归 base case 的取反作为循环条件。
- 将 base case 外的每一步都原封不动地复制过来。
- 对于传入递归函数的每个实参,定义新的变量存储计算后的值。
- 更新函数参数。
- 在循环外返回 base case 中的返回值。
对于 isEven 的优化结果如下:
const isEven = (n: number, even = true) => {
while (!(n === 0)) {
const p0 = n - 1
const p1 = !even
n = p0
even = p1
}
return even
}看上去,尾递归优化似乎与 TCO 有一定区别,实际上,从底层来看,他们都把调用指令改写为跳转指令,尤其是上述尾递归优化中的第五步,可以很明显地看出这正是在通过覆盖函数原有参数以实现帧复用。
回到最初,由于 reduce 的作用与循环类似,所以其实现天然符合尾递归形式。在 Kotlin 中,我们可以通过添加 tailrec 使 Kotlin 编译器应用尾递归优化,此时,尾递归将变为「伪递归」,递归变为循环,call 变为 jmp,递归自然是假的了。
那么,我们是否应该将一切递归函数改为尾递归形式呢?首先,我认为尾递归是一种迫不得已的方案:即要性能,又必须遵循不可变规则,于是只能牺牲递归原本的简便,最后再借助编译器优化完成改写;其次,尾递归优化后性能并不一定更强,不考虑实际情况的优化属于过度优化行为;最后,TCO 会破坏调用栈信息,这也许会影响调试。
综上,爱用啥用啥,代码是给人看的,写得舒服最重要。
总结
其实写这篇文章的初心真的只是想吐糟一下 JS 中的正则表达式,再简单讲讲函数与递归,但不知不觉间就把以前基本不会的三门函数式语言加上了,至少,现在不会对他们感到陌生了。再之后又基本明白了 TCO 的原理,也愈发认识到汇编知识的不可或缺。
真是有趣啊。